Entscheidungsregeln

Die Bayes-Regel (Erwartungswertregel) setzt eine risikoneutrale Grundhaltung des Entscheidungsträgers voraus, weshalb die bekannten Wahrscheinlichkeiten über das Eintreffen von Umweltzuständen mit den Ergebniswerten je Alternative multipliziert und je Alternative addiert werden. Das Ergebnis ist der Erwartungswert, anhand dessen die Entscheidung zu treffen ist.

Bei der μ-σ-Regel ist die Berechnung der Standardabweichung, d. h. die Streuung der Wahrscheinlichkeitsverteilung zu werten, so dass je nach Gewichtung dieses Abweichungsmaßes von Risikoaversen (μ-2σ) oder Risikofreudigen (μ+σ) gesprochen werden kann.

Das Bernoulli-Prinzip ordnet den einzelnen Werten einer Ergebnismatrix gesondert Nutzenwerte anhand einer Nutzenfunktion zu, so dass auch hier die Entscheidung je nach Nutzenpräferenz des Trägers ausfällt.

Nach der Maximax-Regel wählt der Entscheidungsträger diejenige Alternative, die bei dem jeweils günstigsten Umweltzustand noch das beste Ergebnis liefert (Maximierung der Zeilenmaxima). Es handelt sich hier um eine äußerst optimistische Entscheidung.

Nach der Minimax-Regel wählt der Entscheidungsträger diejenige Alternative, die bei Eintreten des ungünstigsten Zustandes noch die besten Ergebnisse liefert (Maximierung der Zeilenminima). Dies entspricht einer pessimistischen Haltung.

Nach der Hurwicz-Regel (Optimismus-Pessimismus-Regel) wird eine Mischform aus den ersten beiden Regeln durch einen Faktor λ eingeführt, der als Optimismusparameter bezeichnet wird. Je größer λ ist, desto eher tendiert diese Regel zum Maximaxprinzip und umgekehrt.

Nach der Savagne-Niehans-Regel, der Regel des kleinsten Bedauerns, soll der maximale Nachteil, der sich durch eine falsche Entscheidung ergibt, noch minimiert werden. Es handelt sich also um eine äußerst pessimistische, risikoaverse Grundeinstellung.

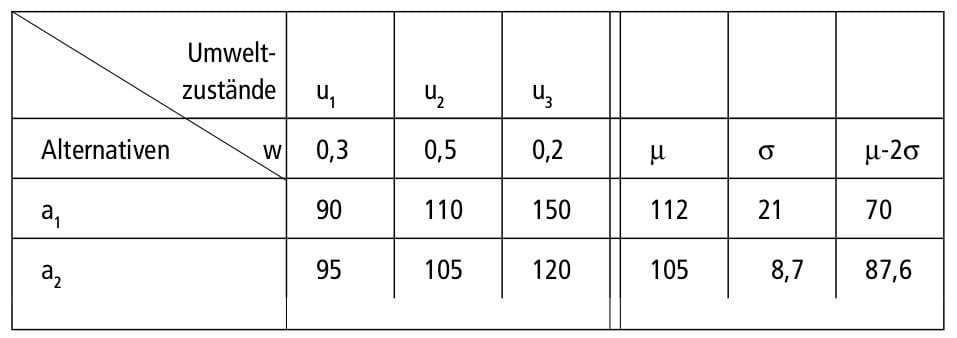
Abb. E-4: Beispielrechnung für eine Entscheidung bei Risiko

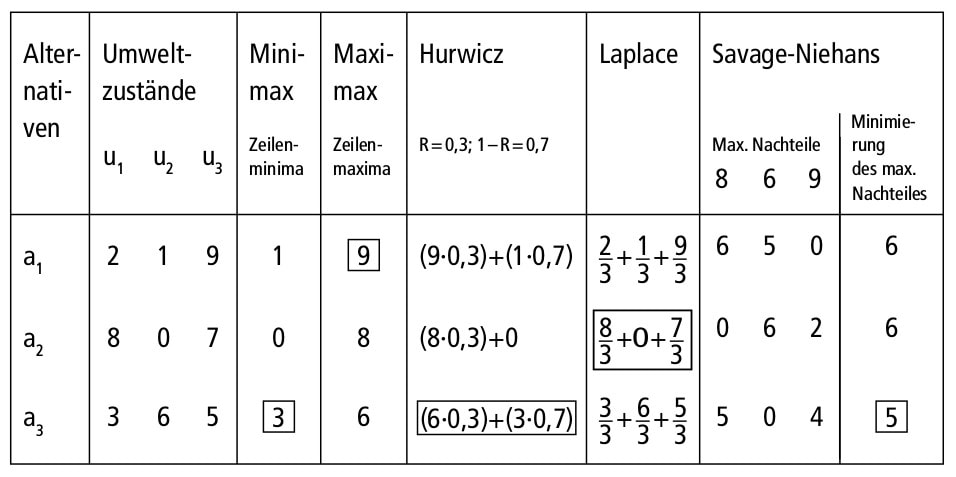
Abb. E-5: Beispielrechnungen für eine Entscheidung bei Ungewissheit