Bewertung und Sensitivitätsmaße von Anleihen als Grundlage für das Laufzeitenmanagement

Anleihemärkte sind spannender, als es auf den ersten Blick erscheint. Wer sein Anleihenportfolio steuern will, muss die wichtigsten Kennziffern dazu verstehen. "Duration" und "Konvexität" tauchen als Schlagworte auf. Wer sie kennt, kann Zinsänderungsrisiken minimieren beziehungsweise gezielt Kurssicherung betreiben ("Hedging") oder direkt auf Kursgewinne setzen.

Im Folgenden werden daher Bewertung und Kurssensitivität von Anleihen durchleuchtet und auf ihre Praktikabilität für den Anleger hin abgeklopft. In einem zweiten Teil geht es dann um Hedging- und Spekulationsstrategien.

Kurs

Doch zunächst geht es um den Kurs von Anleihen: Wer verstanden hat, wie sich Kurse bei Anleihen bilden, kann von da ausgehend auch alle anderen Effekte ableiten. Die Argumentationslinie folgt hier beispielhaft den Staatsanleihen von Industriestaaten, da diese in aller Regel die Funktion einer Benchmark besitzen.

Grundlage bildet die sogenannte "Barwertmethode": Der Wert der Anleihe heute entspricht dem Wert der zukünftigen Zahlungsströme, abgezinst auf heute Bekannt sind:

• Der Rückzahlungskurs K (auch: Nominalwert), der sich in der Regel auf 100 beläuft;

• die Restlaufzeit T der Anleihe;

• die Höhe der Kupons c und deren Auszahlungszeitpunkte (hier: jährliche Auszahlung);

• die je nach Zahlungszeitpunkt unterschiedlichen Zinssätze, die sich je nach Laufzeit aus der Zinsstrukturkurve ergeben

Gesucht wird der Kurs der Anleihe.

Beispiel

Bei einer Anleihe mit Rückzahlungskurs 100 und einer Restlaufzeit von fünf Jahren ergibt sich (beispielhaft) ein aktueller Kurs von 100,50. Hierzu werden die einzelnen Zahlungen (Kupons und Rückzahlungswert) laufzeitenkongruent auf den Zeitpunkt der Bewertung abgezinst (vgl. Schaubild 1). Konkret heißt dies: Ein in einem Jahr zur Auszahlung kommender Kupon wird mit dem Einjahreszinssatz diskontiert, ein in zwei Jahren anstehender Kupon mit dem Zinssatz für eine zweijährige Laufzeit usw.

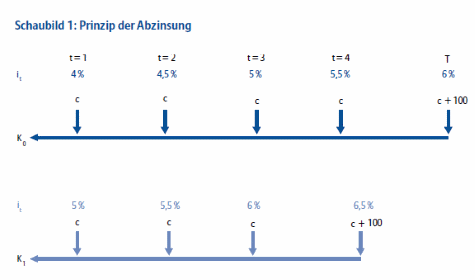
Beispiel 1: Zeiteffekt

Leider nein. Der Zeiteffekt macht sich bemerkbar. Aus der zuerst fünfjährigen ist eine vierjährige Anleihe geworden. Bei einer "normalen" Zinsstrukturkurve sinken die Abzinsungsfaktoren im Zeitverlauf. Bei einer anfänglich über pari notierenden Anleihe steigen die Kurse zunächst und nähern sich dann zur Endfälligkeit hin dem Rückzahlungskurs an. Fachleute sprechen von dem "Rolling- Down-The-Yield-Curve-Effekt", dem "Herunterrollen auf der Zinsstrukturkurve".

Beispiel 2: Zinseffekt

Gleiche Anleihe, gleicher Anfangskurs. Aber: Nach einem Jahr ist die Anleihe nur noch 98,44 wert. Was ist passiert?

Zwar wäre der Kurs der Anleihe allein durch den "Roll-Down-Effekt" auf 102,01 gestiegen. Die Zinsstrukturkurve hat sich aber in der Zwischenzeit nach oben verschoben, das heißt, die Zinsen sind über den gesamten Laufzeitenbereich gestiegen. Würde zum Beispiel der anfänglich in zwei Jahren fällige Kupon statt mit 4,5 % mit 4 % abgezinst (Zeiteffekt), so wird er wegen des allgemeinen Zinsanstiegs jetzt mit 5 %, dem neuen Einjahreszins, abgezinst. Der Diskontfaktor ist gestiegen. Der Risikofall einer Zinsänderung ist eingetreten.

Bei (erwarteten) Zinsänderungen stellt sich immer die Frage: Wie stark steigt / fällt der Anleihepreis, wenn das Renditeniveau fällt / steigt?

Das Zinsänderungsrisiko ergibt sich nur, wenn die Anleihe nicht bis zur Endfälligkeit gehalten wird. Anders kann es auch eine Chance sein: Sinken die Zinsen am Kapitalmarkt, kommt es zu zwischenzeitlichen Kursgewinnen.

Wie stark aber können diese Auswirkungen auf die Kurse - for good or for bad - sein? Welche Risiken geht der Investor ein, welche Chancen bieten sich ihm? Es geht um die Sensitivität, mit der Anleihen auf Zinsänderungen reagieren. Ein wichtiges Maß für die Kurssensitivität von Anleihen ist die Duration.

Duration

Für die Duration gibt es eine Vielzahl an Definitionen. Die gebräuchlichste ist die hier verwendete Macaulay-Duration (vgl. Kasten 3). Konzeptionell kann die Duration nach zwei inhaltlich verwandten Lesarten interpretiert werden. Sie entspricht:

• der gewichteten Bindungsdauer der Zahlungsströme einer Anleihe, wobei die Bindungsdauer jeder Zahlung mit ihrem Anteil am Barwert der Anleihe gewichtet wird;

• der durchschnittlichen Laufzeit einer Anleihe, unter Berücksichtigung aller anfallenden Cashflows, das heißt der zufließenden Kupons und des Rückzahlungsbetrages.

Im Klartext heißt dies: Hat eine Anleihe mit einer Laufzeit von fünf Jahren zum Beispiel eine Duration von vier Jahren, dann ist das Anfangskapital durchschnittlich vier Jahre gebunden.

Aus der Duration lässt sich durch einfache Umformung die Kurssensitivität errechnen, mit der eine Anleihe auf eine Renditeänderung reagiert. Dazu wird in der Regel die modifizierte Duration genommen (vgl. Kasten 4). Bei einer modifizierten Duration von vier fällt der Kurs einer Anleihe um 4 %, wenn die Zinsen um 1 % steigen.

Die (modifizierte) Duration lässt sich auch auf ein gesamtes Anleihenportfolio, zum Beispiel einen Rentenfonds, anwenden. Sie gibt dann Antwort auf die Frage: Wie stark steigt / fällt mein Rentenportfolio im Wert, wenn die Zinsen um einen bestimmten Satz fallen beziehungsweise steigen?

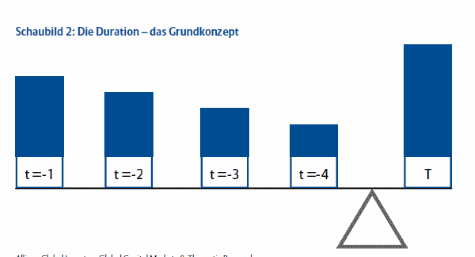
Eigenschaften der Duration

Die Duration gleicht einer Waage, welche die Zahlungsströme im Gleichgewicht hält (vgl. Schaubild 2). Sie entspricht genau dem Gleichgewichtspunkt zwischen den einzelnen Kuponzahlungen und dem Rückzahlungskurs. Diese bildhafte Darstellung, welche die Duration als Maß für die gewichtete Bindungsdauer des eingesetzten Kapitals versinnbildlicht, verdeutlicht deren Eigenschaften:

• Da die Cashflows auf den Barwert zum Zeitpunkt der Berechnung abgezinst werden, gilt: Je früher die Auszahlungen anstehen, desto geringer ist ihr Abzinsungsfaktor und desto größer ist ihr jeweiliges Gewicht.

• Je kleiner der Kupon, desto größer ist die Duration, da der Rückzahlungskurs relativ an Gewicht gewinnt. Um im (Schau-) Bild zu bleiben: Der Gleichgewichtspunkt wandert weiter nach rechts. Im Spezialfall des Zero-Bonds entspricht die Laufzeit exakt der Duration. • Anleihen haben keine konstante Duration. Diese ist vielmehr von den Marktgegebenheiten abhängig. Dazu gehören die Höhe der Kupons, die Restlaufzeit und die (aktuelle) Zinsstrukturkurve. Ein bedeutsamer Punkt gerade für Sicherungsstrategien, da die Maßnahmen zur Sicherung des Kurswertes mit der Veränderung der Duration immer wieder adjustiert werden müssen.

• Mit zunehmendem Zinsniveau am Kapitalmarkt nimmt die Duration ab, da die zukünftigen Cashflows stärker abgezinst werden.

• Zwischen den Kuponterminen nimmt die Duration mit der Zeit linear ab. Um einen Kupontermin herum kommt es zu einem Sprung in der Duration. Der alte Gleichgewichtspunkt verschiebt sich nach rechts.

Konvexität

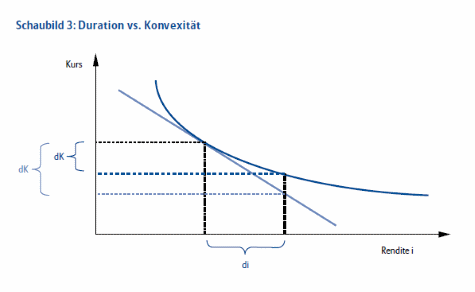
Allerdings: Die Duration ist nur ein Näherungsmaß für kleine Zinsänderungen. Kommt es zu größeren Anpassungen, erfasst sie die Kursänderungen nur ungenau, denn sie unterstellt einen linearen Zusammenhang von Zins- und Kursänderung. Tatsächlich ist dieser aber konvex. Die Duration führt daher zu Ungenauigkeiten, die umso größer ausfallen, je größer die Zinsänderung ist (vgl. Schaubild 3).

Wenn die Zinsen fallen, ist die über die Duration bestimmte Kursänderung kleiner als die tatsächliche. Wenn die Zinsen steigen, weist die Duration eine größere als die tatsächliche Kursänderung aus. Das exakte Maß für die Kurssensitivität ist die Konvexität.

Aus Schaubild 3 werden die Eigenschaften der Konvexität deutlich:

• Mit steigender (interner) Rendite sinkt die Konvexität des Bonds, entsprechend der Steigung der Kurve.

• Bei gegebener Rendite und Restlaufzeit ist die Konvexität umso größer, je niedriger der Kupon ist. Entsprechend reagiert eine Null-Kupon-Anleihe am stärksten auf eine Renditeänderung.

• Mit zunehmender Duration nimmt die Konvexität eines Bonds in steigendem Maß zu. Das heißt: Tauscht ein Investor einen Bond gegen einen anderen mit doppelter Duration, dann nimmt die Konvexität um mehr als das Doppelte zu. Das heißt auch: Die Messungenauigkeit der Duration gegenüber dem Konvexitätsmaß steigt.

Gerade bei einem asymetrischen Risikoprofil, wie es typischerweise in einem Niedrigzinsumfeld vorherrscht, ist Laufzeitenmanagement wichtig.

Dabei kann es vorteilhaft sein gezielt auf Laufzeiten, die zum eigenen Anlagehorizont passen, zu setzen, um das Durationsrisiko zu begrenzen und um dennoch eine Rendite zu erzielen, die überhalb des Geldmarktes liegt.

Entscheidende Einblicke für vorausschauende Anlagestrategien! Wir sind überzeugt: Nur wer heute schon versteht, wie sich unser Leben in Zukunft entwickelt, kann vorausschauend investieren. Allianz Global Investors ist mit fachübergreifenden Kompetenzteams und Spezialisten global vertreten. Ausführliche Informationen erhalten Sie unter www.allianzglobalinvestors.de.

Der obige Text spiegelt die Meinung des jeweiligen Kolumnisten wider. Die finanzen.net GmbH übernimmt für dessen Richtigkeit keine Verantwortung und schließt jegliche Regressansprüche aus.